摘要
压气机的复杂流动中包含流动分离和逆压力梯度,基于雷诺平均湍流模型的数值仿真流场通常会或多或少偏离实验测量结果。为了提高流场预测精度,减少数值仿真与实验测量之间的偏差,提出了一种基于深度神经学习和ℓ1正则的实验数据驱动的压气机流场预测方法,为获得高可信度的流场,校正了进口边界条件和湍流模型参数。独立使用了S-A和SST湍流模型性相互验证预测结果,并使用敏感性分析方法获得关键参数的贡献。结果显示本文提出的算法可以减小约70%的预测偏差,两种湍流模型预测出的流场几乎相同即预测结果基本独立于湍流模型。进口边界条件的修正主要减小了前半弦长的预测偏差,而湍流模型的修正主要减小了吸力面尾缘流动分离的过渡预测。
论文标题
Experimental data-driven flow field prediction for compressor cascade based on deep learning and ℓ1 regularization
作者
LIU Tantao (刘锬韬), GAO Limin (高丽敏), LI Ruiyu (李瑞宇),
作者单位
Northwestern Polytechnical University (四色AV
)
出版信息
Journal of Thermal Science, Vol 33, pages 1867–1882, (2024)
//doi.org/10.1007/s11630-024-2035-8
研究背景
对航空发动机日益增长的更高性能、可靠性和经济性的需求推动了流场预测技术的进步。发动机中的压气机用于来流空气减速增压,对发动机的安全性、推力和油耗至关重要。压气机中存在流动分离和强逆压梯度。高负荷压气机中的流动更加复杂。压气机测试可以提供真实的运行数据,是评估压气机性能的金标准。测试测量数据来自真实的压缩机流场,因此与数值模拟数据相比,它是高保真数据。然而,安装在测试台上的传感器或探头的数量是有限的,在测试过程中只能测量几种物理量。相比之下,基于计算流体动力学(CFD)的流场数值模拟可以提供整个流场的所有物理量。然而,使用湍流模型的CFD结果往往与实验数据存在偏差,特别是对于复杂的流动,如压气机中的流动,如图1所示。在非设计工况下,偏差往往更为明显,不同的湍流模型获得的结果也有明显差别。有必要采取措施提高CFD预测精度。当前基于CFD的研究中,实验测量数据主要用于验证CFD计算结果的大致正确性,没有参与具体的预测过程,宝贵的实验测量数据被利用的并不充分。由此开展了实验数据驱动的压气机叶栅流场增强预测研究,以提高压气机叶栅流场的预测精度。
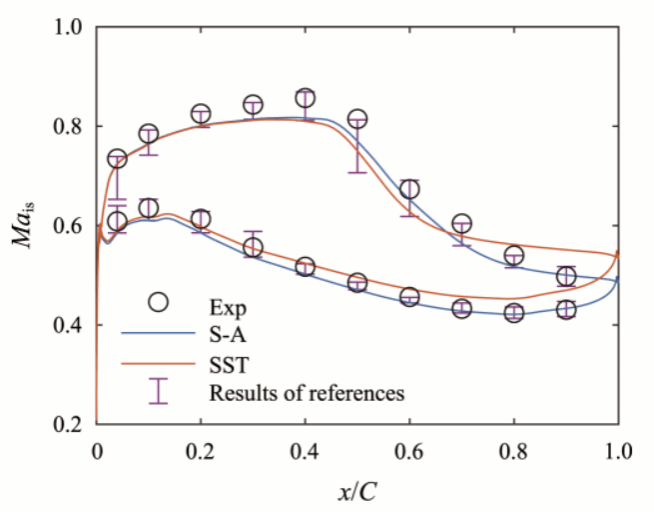
图1 通常的CFD预测结果与实验有一定差异
研究亮点
1)基于深度学习和ℓ1正则的实验数据驱动流场预测框架构建
首先分析了造成压气机叶栅流场预测结果与实验测量结果有偏离的原因:一方面是基于雷诺平均的湍流模型对于分离流动预测精度十分有限,导致分离区预测不准确;另一方面来源实验过程中,叶栅吹风实验时风洞壁面效应导致实验的真实来流参数偏离给定的工况参数,而CFD流场数值计算时使用的给定的工况参数。由此,制定了通过校正来流边界条件和湍流模型系数来融合实验测量数据和数值模拟数据的增强预测方案。构建了基于深度学习和ℓ1正则的实验数据驱动流场预测框架,将预测问题转化为一个优化问题,如图2所示:使用深度神经网络构建待校正系数和与预测结果之间的映射关系,设计了包含待校正参数、预测偏差和ℓ1正则项的损失函数,利用自动微分工具使用梯度下降算法求取损失函数的最小值,当损失函数达到最小时,系数为最优解。这种框架的好处是分割了流场数值计算与优化过程,流场计算可以使用大型工作站大规模并行进行,而优化过程可以使用普通计算机进行,而且可以根据研究需求自由设计损失函数。
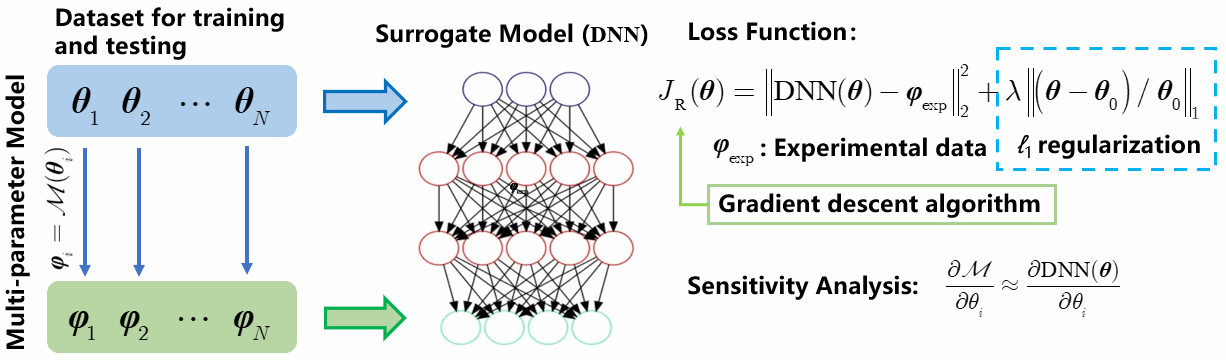
图2 基于深度学习和ℓ1正则的实验数据驱动流场预测框架
2)通过ℓ1正则项防止参数过度修正和局部最优解
在损失函数中添加了ℓ1正则项,该项为参数相对修正量的ℓ1范数,作用为防止对参数的过度修正,ℓ1范数具有天然稀疏性,常在机器学习算法中用于防止过度拟合,在此用于防止过度校正。因为神经网络模型本身具有一定误差,实验测量结果也具有一定不确定度,若没有正则项约束,模型误差及测量噪声会严重影响校正过程,造成过度预测,类似于过拟合。
添加ℓ1正则项的另一个作用是避免局部最优解,梯度下降法一个缺点是对于非凸问题容易收敛到局部最优,ℓ1正则项本身的凸的,选择适宜的正则系数可以使损失函数近似为凸函数,从而避免得到局部最优解,如图3所示,并且可以减小优化迭代次数。
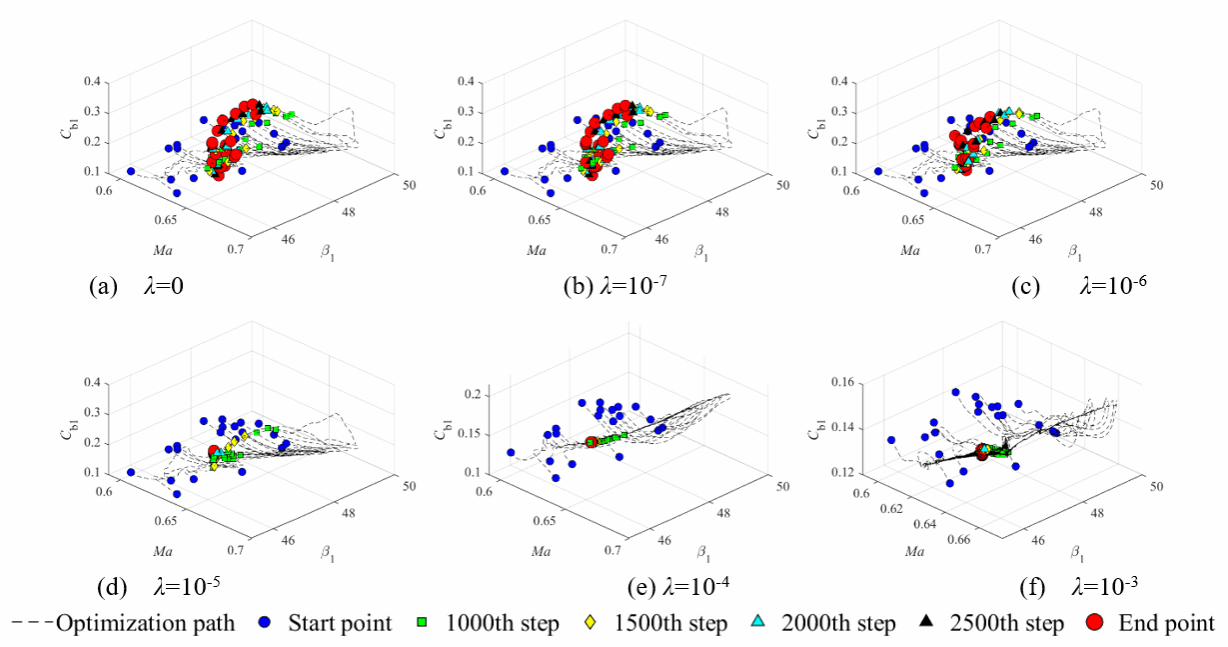
图3 合理选择正则系数可避免局部最优
3)获取高保真且与湍流模型无关的预测流场
在获得损失函数的极小值后,利用最优参数重新进行流场数值计算,即可获得高保真且与湍流模型无关的增强预测流场。图4显示了设计工况时,使用原始参数(Default)、仅校正来流边界条件(BC)和校正了进口边界条件和湍流模型系数(All)的计算结果叶栅表面等熵马赫数分布。预测时使用了两种湍流模型,可以看出进行实验数据驱动预测后,两种湍流模型结果几乎完全一致,且与实验结果高度相符。图5进一步显示了四种工况参数校正前后预测相对偏差的分布情况,预测偏差总体减小了约70%。图6、图7、图8分别展示了湍流模型参数校正前后流场参数的分布情况,校正后的吸力面分离区减小,分离点后移。尽管使用了两种不同的湍流模型,在校正湍流模型后,两种模型的预测结果基本是一致的,由此验证增强预测流场基本实现了结果与湍流模型的选择无关。
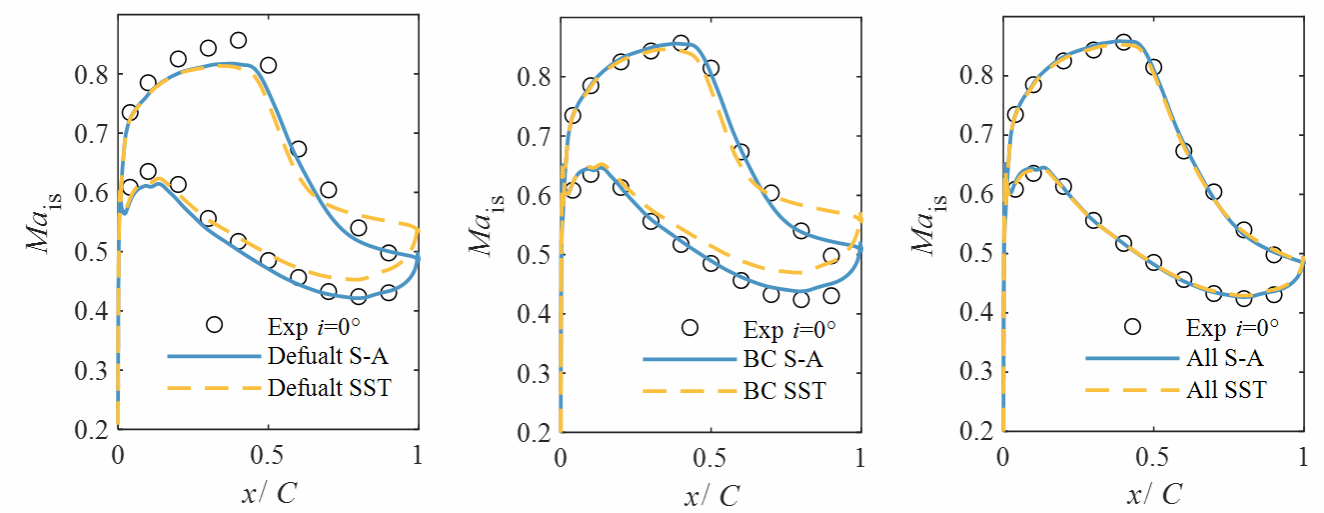
(a)原始参数 | (b)仅校正来流边界条件 | (c)校正所有参数 |
图4 原始预测结果与增强预测结果对比
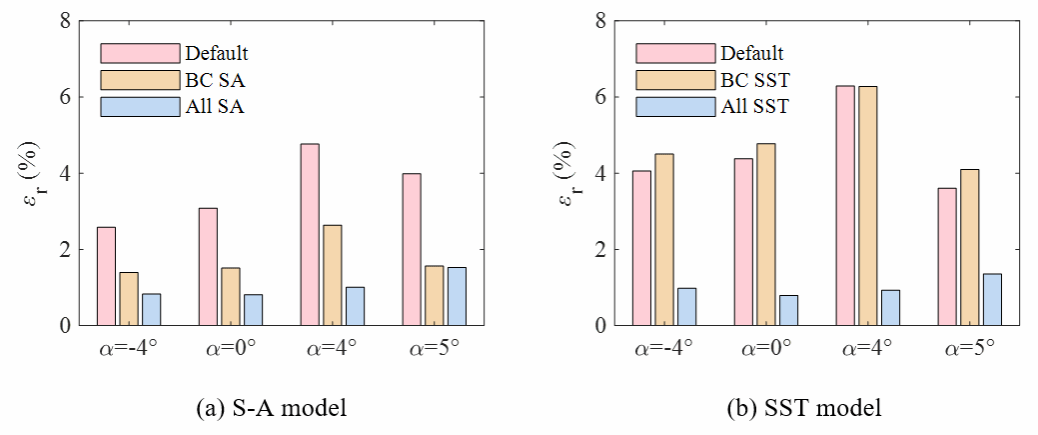
图5 参数校正前后两种湍流模型预测偏差
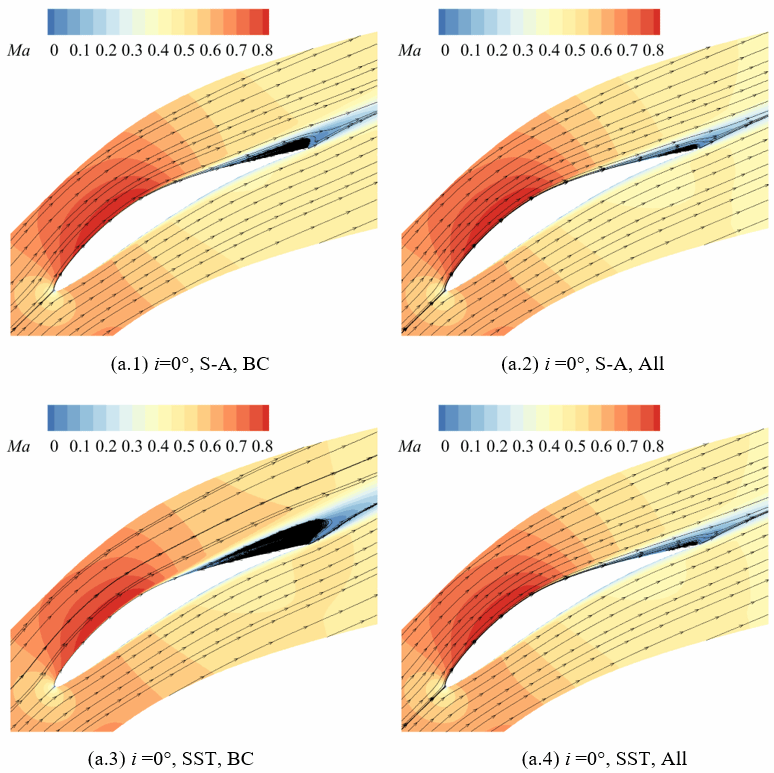
图6 湍流模型参数校正前后分离区预测情况
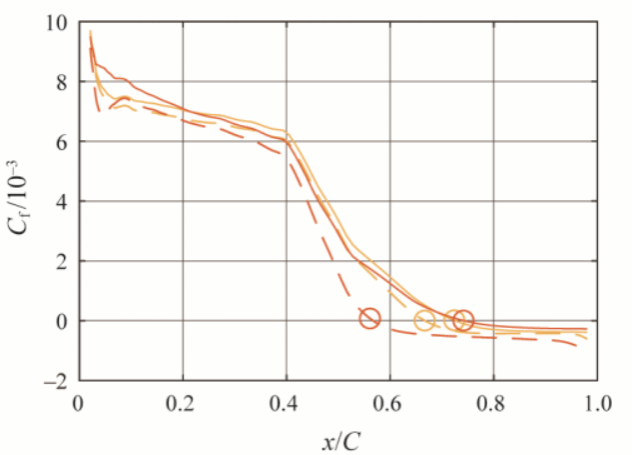
图7 湍流模型参数校正前后吸力面剪切力系数分布及分离点(圆圈)
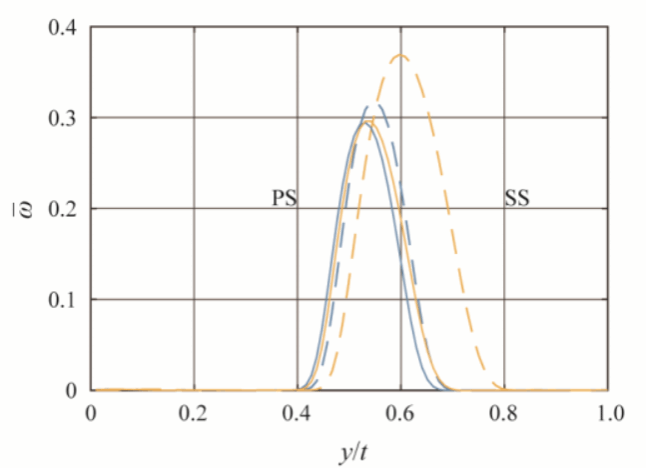
图8 湍流模型参数校正前后的尾迹损失系数分布
4)校正参数的敏感性分析
参数校正的过程中主要修正了来流马赫数Ma、进气角i和S-A模型中Cb1和SST模型中a1系数,其他参数由于对校正结果影响较小没有被修正,为了显示被修正的系数的在校正结果中起到的作用,定义了参数的相对敏感性RS和绝对敏感性AS,对被修正参数进行了敏感性分析。
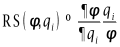
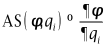
可以看出进口马赫数影响叶片表面全域,进气角主要影响前半弦长,而湍流模型系数主要影响后半弦长区域。
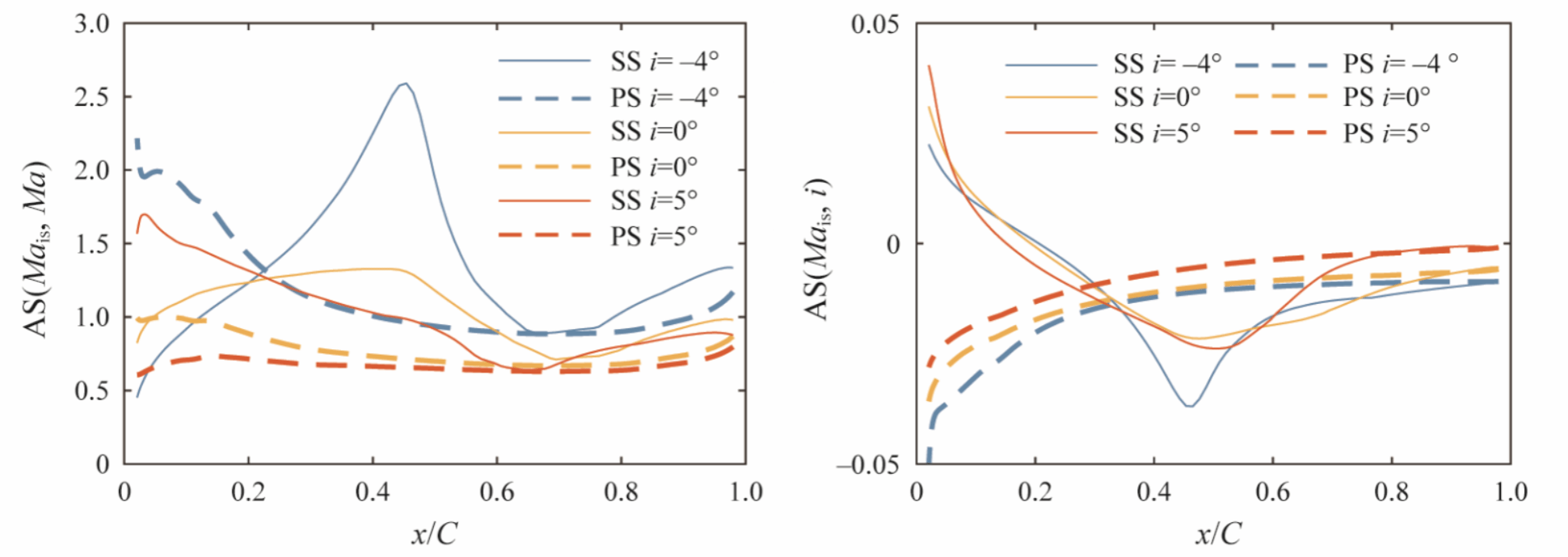
图9 进口参数的绝对敏感度
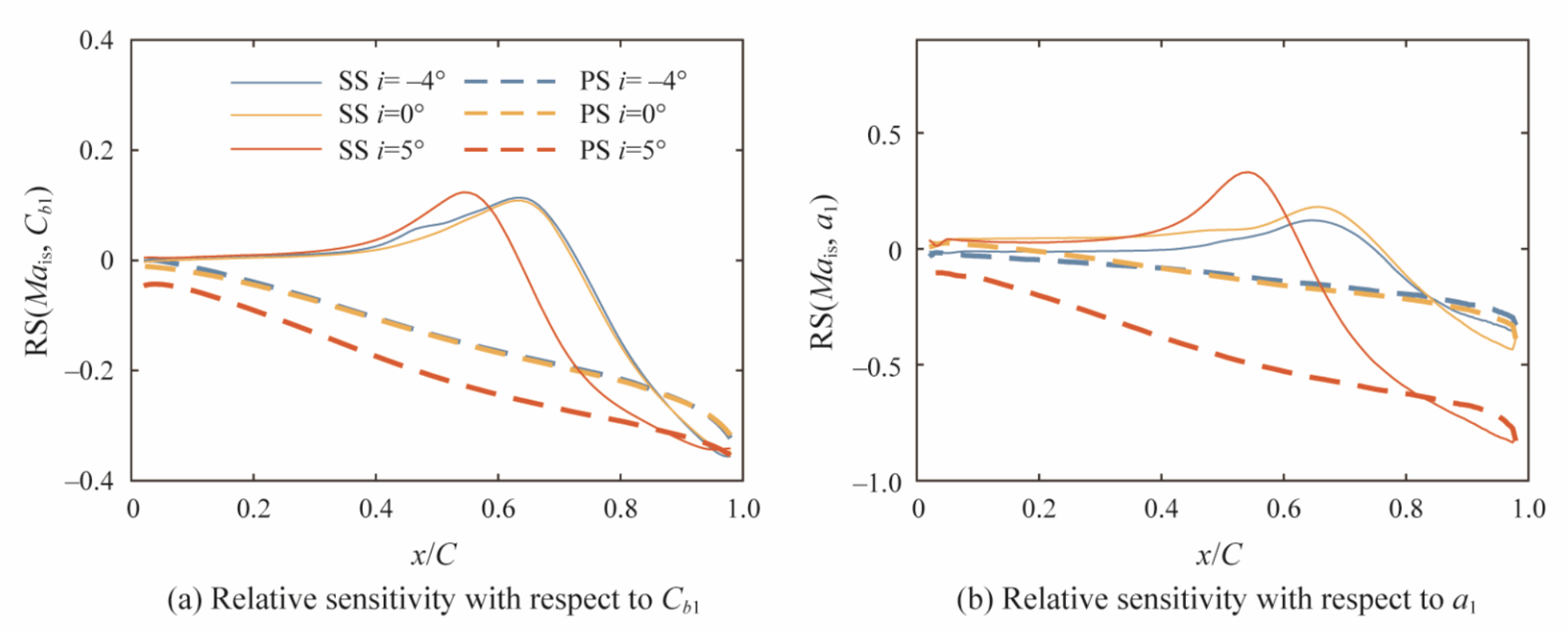
图10 湍流模型关键系数的相对敏感度
研究结论
所提出的基于深度学习和ℓ1正则化的实验数据驱动流场预测方法可以为压气机叶栅流提供高保真的流场数据。ℓ1正则化有助于提高非线性损失函数的凸性,避免局部极值问题。入口边界条件和湍流模型参数的校准可以将预测误差降低近70%。边界条件校正减小了弦前半部分的预测误差。校准的湍流模型解决了尾缘附近吸力面上流动分离区的过高预测问题。两种湍流模型预测的流场几乎相同;即它们独立于特定的湍流模型。沿叶片表面等熵马赫数的敏感性分析表明,入口马赫数影响整个弦;然而,入射角主要影响前半弦。主要修改的湍流模式参数Cb1和a1主要影响弦的后半部分。
主要作者简介
刘锬韬(第一作者),男,博士研究生,主要从事压气机气动热力学流场预测及数据同化研究。
高丽敏(通讯作者),女,教授,博士,团队负责人,主要从事轴流与离心叶轮机复杂流场的数值仿真 、高效节能叶轮机械气动设计、计算流体动力学理论及工程应用、先进流动显示与测量技术、推进系统气动热力过程模拟分析。
李瑞宇,女,教授,博士,主要从事压气机高保真数值方法、压气机非定常实验测量技术以及压气机内流试验/数值数据挖掘和融合方面的研究工作。
审核:徐永超